jeudi 31 mars 2016

Illustration tirée de l'encyclopédie Brockhaus et Efron (1890-1907) représentant deux globes terrestresentourés de diverses formes géométriques.

Ce formulaire de géométrie classique récapitule diverses formules reliant algébriquement des mesures de longueur, d'aire ou de volume pour des figures de géométrie euclidienne.

Sommaire

[masquer]

Figures du plan[modifier | modifier le code]

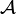Nom	Périmètre $p\,$	Aire intérieure $\mathcal A$	Relations supplémentaires
Carré	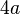$4 a\,$	$a^2\,$	$d = a\sqrt{2}$
Rectangle	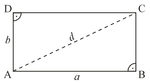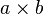$2(a+b)\,$	$a\times b$	$d = \sqrt{a^2+b^2}$
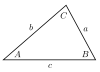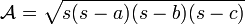
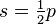Triangle	$a+b+c\,$	$\tfrac{1}{2}b \times h$	$\mathcal A = \sqrt{s(s-a)(s-b)(s-c)}$ où $s=\tfrac{1}{2}p$ (formule de Héron)
Triangle équilatéral	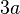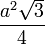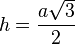$3a\,$	$\frac{a^2\sqrt{3}}{4}\,$	$h= \frac{a\sqrt{3}}{2}$
Triangle isocèle rectangle	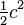$(2+\sqrt{2})c$	$\tfrac{1}{2}c^2$	$d = c\sqrt{2}$
Losange	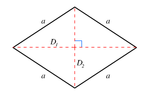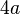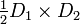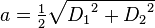$4 a\,$	$\tfrac{1}{2}D_1\times D_2$	$a = \tfrac{1}{2}\sqrt{{D_1}^2+ {D_2}^2}$
Parallélogramme	$2(a+b)\,$	$a\times h$
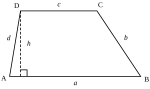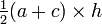Trapèze	$a+b+c+d\,$	$\tfrac{1}{2}(a+c)\times h\,$
Disque	$2\pi r\,$	$\pi r^2\,$
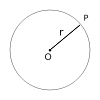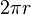Ellipse	(non algébrique)	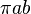$\pi a b\,$	(voir ci-dessous)

La lettre

\pi

désigne la constante d'Archimède qui vaut environ 3,14.

Triangle rectangle

Théorème de Pythagore: Dans un triangle 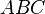$ABC$ rectangle en $C$ , les longueurs des côtés sont reliées par la formule :; $AB^2 = AC^2 + BC^2\ .$

Configuration de Thalès

Théorème de Thalès: Dans un triangle 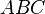$ABC$ non plat, si une droite parallèle à $(BC)$ coupe $(AB)$ en $D$ et coupe $(AC)$ en $E$ alors les égalités suivantes sont vérifiées :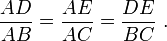; $\frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC}\ .$

Nom	Aire de la surface	Volume intérieur	Relations supplémentaires
Cube	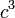$6 c^2\,$	$c^3\,$	$\mathcal D = c\sqrt{3}$
Pavé droit	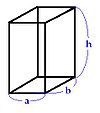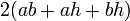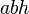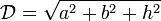$2(ab+ah+bh)\,$	$abh\,$	$\mathcal D = \sqrt{a^2+b^2+h^2}$
Prisme droit	P base fois h	$\mathcal B\times h$
Cylindre de révolution	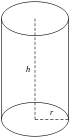extrémités : $2\times \pi r^2$ surface latérale : 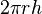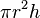$2\pi r h\,$	$\pi r^2 h\,$
Pyramide		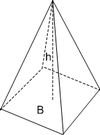$\tfrac{1}{3}\mathcal B\times h$
Tétraèdre régulier	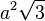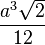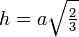$a^2\sqrt{3}$	$\frac{a^3\sqrt{2}}{12}$	$h = a\sqrt{\tfrac{2}{3}}$
Cône de révolution	base : $\pi r^2$ surface latérale : 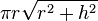$\pi r \sqrt{r^2 + h^2}$	$\tfrac{1}{3}\pi r^2 h$
Sphère	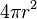$4\pi r^2\,$	$\tfrac{4}{3}\pi r^3$
Calotte sphérique	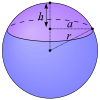base : $\pi a^2\,$ surface courbe : 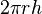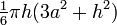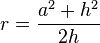$2\pi r h\,$	$\tfrac{1}{6}\pi h(3a^2+h^2)$	$r = \frac{a^2+h^2}{2h}$
Ellipsoïde	(non algébrique)	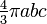$\tfrac{4}{3}\pi abc$
Tore ouvert	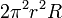$4 \pi^2 r R\,$	$2\pi^2 r^2 R\,$	2